Understanding Data Structures and Their Operations in Linear Algebra
Written on
Chapter 1: Introduction to Data Structures
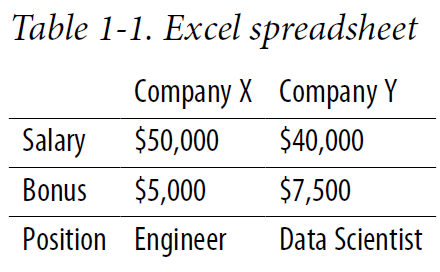
The fundamental data structure in applied linear algebra is undoubtedly the matrix, which is essentially a two-dimensional array of numbers. Each element can be accessed through its corresponding row and column indices. For instance, consider an Excel spreadsheet where two companies, Company X and Company Y, are listed in rows, and various features such as salary, bonuses, or job positions are represented in columns, as illustrated in Table 1–1.
This tabular format is particularly effective for managing and referencing data, allowing users to pinpoint specific entries, such as the starting salary offered by Company X. Matrices serve as versatile tools for organizing numerical data. In the realm of deep learning, they play a crucial role in representing both datasets and the weights within neural networks. For example, a dataset about lizards could include attributes like length, weight, speed, and age, structured neatly within a matrix where each row corresponds to a specific lizard and each column to a feature like age.
However, unlike the detailed information provided in Table 1–1, a matrix focuses solely on numerical values, relying on the user to keep track of the relationships between the rows and columns and the units used. As depicted in Figure 1–1, it's assumed that the age of each lizard is measured in years, with the notable Komodo Ken weighing in at an impressive 50 kilograms.
But why opt for matrices when tables can convey more information? In both linear algebra and deep learning, operations such as addition and multiplication can be efficiently executed on data when it's strictly numerical. Much of linear algebra revolves around the unique characteristics of matrices and the operations applicable to these data structures.
Section 1.1: Vectors and Their Role
Vectors, which are essentially one-dimensional arrays of numbers, can be viewed as a specific type of matrix. They are particularly useful for representing individual data points or weights in linear regression models. This section delves into the properties and operations related to matrices and vectors.
Subsection 1.1.1: Operations on Matrices
Matrices can undergo addition, subtraction, and multiplication, though division isn't applicable. Instead, there's a related concept known as inversion. To add two matrices A and B, one iterates through each index (i, j) of the matrices, sums the corresponding entries, and assigns the result to a new matrix C at the same index (i, j), as shown in Figure 1–2.
This method indicates that matrices of different shapes cannot be added together, as certain indices may not align. Additionally, the resulting matrix C retains the same dimensions as A and B. Beyond addition, matrices can also be multiplied by scalars, which involves multiplying each entry of the matrix by the scalar, maintaining the shape of the matrix, as illustrated in Figure 1–3.
These operations lead to matrix subtraction, as subtracting A - B can be rephrased as A + (-B), where -B represents the product of -1 and matrix B. The process of multiplying two matrices becomes more intricate. To define the matrix product A · B, we consider the value at index (i, j) as the sum of the products of the entries in the ith row of A and the jth column of B. This multiplication is only valid when the rows of A and the columns of B align in length, which leads to an indexing error if they do not.
Furthermore, we utilize the term dimension to indicate the shape of matrices: A has dimensions m by k (m rows and k columns), while B has dimensions k by n. The resulting product will then have dimensions m by n, ensuring an entry for every combination of rows in A and columns in B. It's crucial to note that matrix multiplication is not commutative; hence A · B does not equal B · A.
Chapter 2: Advanced Matrix Operations
This video titled "Data structure operations | tutorial | in hindi part2 - YouTube" provides an in-depth tutorial on various operations involving data structures.
In "What is Stack Data Structure? | Data Structure and Algorithms (DSA) | Part - 1 - YouTube," this video explains the fundamentals of stack data structures in an engaging manner.
One of the critical matrices in linear algebra is the identity matrix, characterized by having 1s along its main diagonal and 0s elsewhere. Denoted as I, this matrix yields the original matrix A when multiplied by it. Experimenting with the identity matrix against different matrices will illustrate why it holds this property.
While division isn't a direct operation for matrices, the concept of inversion exists. The inverse of matrix A, denoted as A−1, is such that AB = BA = I, akin to a reciprocal in arithmetic. For A to be invertible, it must at least be a square matrix. When solving equations like Ax = b for x, we can isolate x as A−1b if A is indeed invertible.