Understanding Bayes' Theorem in the Context of COVID-19 Testing
Written on
Chapter 1: The Challenge of COVID-19 Testing
The ongoing global pandemic has sparked a strong demand for increased testing. However, simply increasing the number of tests conducted does not necessarily improve outcomes. The challenge lies in the occurrence of false positives, particularly when two unlikely events are closely linked.
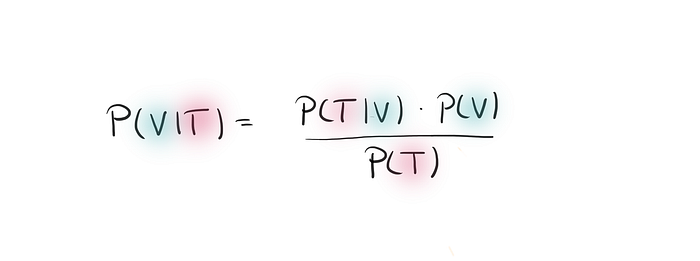
Writer's Note: If you're not interested in the mathematical details, feel free to skip to the conclusion. However, I urge you not to dismiss the validity of current testing methods. There are logical reasons, both practical and mathematical, for why universal testing isn't feasible or effective, which will be discussed here.
Understanding the Testing Framework
Consider a hypothetical individual, whom we will call Sarah. She may either be infected with the virus or not. Upon testing, there are four possible outcomes:
- Sarah is infected and tests positive.
- Sarah is infected but tests negative.
- Sarah is not infected and tests negative.
- Sarah is not infected but tests positive.
Outcomes 1 and 3 indicate correct test results, while outcome 2 poses a risk since Sarah may unknowingly spread the virus, and outcome 4 places Sarah in unnecessary quarantine, despite being healthy.
Most medical tests boast a correctness rate of 90-99%. Here, "correct" has dual meanings:
- A 99% sensitivity means that out of 100 infected individuals, 99 will receive a positive result.
- A 99% specificity means that out of 100 uninfected individuals, 99 will receive a negative result.
It's crucial to note that sensitivity and specificity do not need to be equivalent. Various factors, such as low viral loads or contamination of samples, can lead to inaccuracies, but a detailed medical analysis is beyond the scope of this discussion.
The Role of Bayes' Theorem
To truly understand testing effectiveness, we need to consider the probability of being infected after receiving a positive test result, denoted as the probability of V given T. This calculation utilizes Bayes' Theorem:
Bayes' Theorem allows us to shift our focus from infected individuals to those who have tested positive. The probability of a positive test result encompasses both true positives (infected and tested positive) and false positives (not infected but tested positive).
We can define these probabilities using the principles of conditional probability for sensitivity and specificity. This results in a formula that, while appearing complex, is mathematically sound and relies solely on sensitivity, specificity, and the overall infection rate P(V).
Analyzing the Numbers
Now, let's examine some numerical examples. Below is a simple Python code snippet you can run in a Jupyter Notebook to explore various scenarios:
spec = 0.99
sens = 0.99
infected = 0.001
VgivenT = (sens * infected) / (sens * infected + (1 - spec) * (1 - infected))
print(VgivenT)
With a sensitivity and specificity of approximately 99% and an infection rate of around 0.1%, the probability that someone who tests positive is actually infected is less than 10%. If the infection rate rises to 1%, this probability increases to about 50%, and at 50%, it reaches 99%.
Surprisingly low results emerge, illustrating how conditional probabilities can yield counterintuitive outcomes when dealing with infrequent events.
An Intuitive Perspective
To illustrate this intuitively, consider the U.S. population of around 330 million. If 0.1% are infected, that equates to 330,000 individuals. The remaining 329,667,000 non-infected individuals could yield approximately 3,296,700 false positives, significantly outnumbering actual cases. Conversely, if the infection rate is 1%, the number of false positives aligns more closely with the number of actual infections.
Conclusion
This is why receiving a positive test result with few or no symptoms warrants a retest. The likelihood of multiple false positives is minimal, so two or more consecutive positive results can indicate genuine infection.
Randomly testing everyone is impractical and would likely result in numerous false positives, leading to inconclusive data. Importantly, the mathematics discussed here applies only under the assumption that testing and infection rates are independent, which isn't the case in reality.
Scientists understand this nuance, which is why they focus testing efforts on symptomatic individuals or those with known exposure to infected persons. This targeted approach minimizes false positives and keeps error rates closer to the advertised 1%.
In summary, I do not subscribe to the notion that we are inundated with false positives. The severity of the situation is evidenced by the ongoing fatalities. This discussion aims not to undermine testing efforts but to highlight the sophistication of current testing strategies. Testing is most effective when there is reasonable suspicion of infection, either through close contact or strong symptoms.
This narrative serves as a reminder that increasing the number of tests does not inherently lead to improved outcomes and that statistics can be easily misinterpreted.
The first video titled "False Positives & Negatives for COVID-19 tests | Using Bayes' Theorem to Estimate Probabilities" explains the complexities of testing results and the implications of false positives and negatives.
The second video, "Bayes rule applied to a COVID-19 rapid test," further explores the application of Bayes' Theorem in understanding test results and probabilities.