Exploring the Area of a Rhombus: A Fun Geometry Challenge
Written on
Chapter 1: Introduction to the Puzzle
As I sit here with sunlight streaming through my window, I find myself reflecting on my motivation for writing this article. With exams looming, my enthusiasm for studying is waning, yet I am determined to push through. The question arises: am I writing this blog out of a genuine passion for mathematics, or is there another reason?
Before we delve into the solution, I encourage you to pause and grab some pen and paper. Take a moment to tackle this puzzle on your own. When you're ready, continue reading for the answer!
Section 1.1: Dissecting the Rhombus
Let's take an innovative approach and break the rhombus down into six triangles.
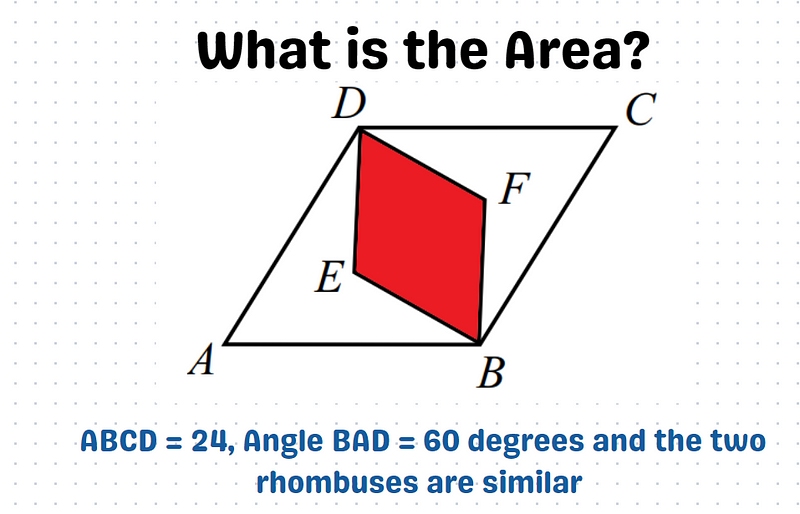
We know that angle ?BAD = 60°, which indicates that triangle BAD is also equilateral. Consequently, triangles AEB, AED, BED, BFD, BFC, and CFD are congruent. This means that these six triangles each occupy the same area. Given that the total area of the rhombus is 24, each individual triangle has an area of...
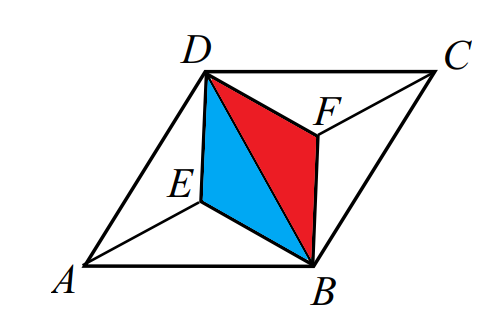
Now, rhombus DEFB consists of two such triangles, leading us to conclude that...
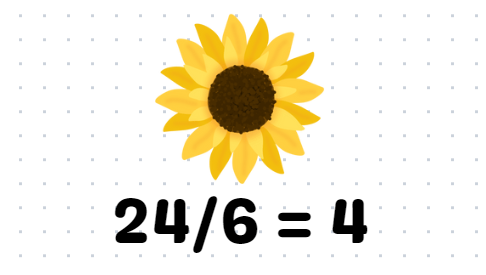
And that gives us our final answer.
Section 1.2: Reflection on the Process
Perhaps the reason for my writing is less important than the impact I may have on you as a reader. What were your thoughts during this puzzle? I would love to hear your insights in the comments!

Math Puzzles
If you're interested in more intriguing math puzzles, consider checking out the best puzzles available on Medium, covering a variety of topics including Algebra, Geometry, and Calculus.
The first video, "HOW TO FIND THE AREA OF A RHOMBUS," provides a detailed explanation of the concepts discussed here.
The second video titled "Area of a Rhombus" further explores techniques and examples in finding areas, making it a valuable resource for visual learners.
Chapter 2: Conclusion
I appreciate you taking the time to read through this puzzle! If you found it insightful, please give it a clap and consider supporting my writing.

If you enjoyed this content, feel free to buy me a coffee—it's a wonderful way to support my work and personal endeavors. Happy solving, Bella!