Exploring the Comparison of 99^100 and 100^99
Written on
Chapter 1: Introduction to the Comparison
At first glance, the question of whether 99 raised to the 100th power or 100 raised to the 99th power is larger may seem straightforward, but the underlying proof is intriguing, particularly its connection to the number 3 (as hinted by the accompanying image). Curious about how this all ties together? Let's delve into the details!
The Mathematical Proof
Both numbers, 99 and 100, share a common relationship. Interestingly, multiplying 100 by 99 yields a total of 9,900, just as 99 multiplied by 100 does. With this in mind, we can reformulate our problem:
“Determine the pair of numbers that together total 9,900, while maximizing their product.”
In mathematical terms, we can express this as:
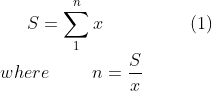
To maximize the function f(x), we need to consider the logarithm of this function, as maximizing the logarithm will yield the same result due to its increasing nature. Thus, we aim to find the value of x that maximizes:
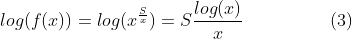
To identify the maxima, we compute the derivative of the function:
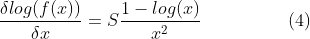
The resulting equation indicates a positive slope when x is less than e, a negative slope when x exceeds e, and a zero slope when x equals e. This implies that log(f(x)) is convex and that a maximum is achieved when x is approximately equal to 2.72. The nearest integer to this is 3! Therefore, using three 3s yields the highest product when the sum is 9,900.
Now, returning to our original comparison, we analyze the values of log(f(x)) at x = 99 and x = 100. Since the function exhibits a decreasing nature beyond e, we conclude that f(99) exceeds f(100).
This completes our mathematical proof.
Unit Tests
To validate our mathematical proof, let’s conduct a simple test with S = 9. We can explore various combinations of numbers that add to 9:
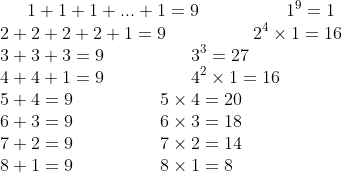
As observed, combining three 3s indeed maximizes the product! Experimenting with other sums, like S = 12, may yield similar results. Notably, the more the numbers diverge from 3, the smaller the product tends to be, reinforcing our earlier findings that 100 yields a lesser product compared to 99.
The Practical Proof
In a Python environment, inputting len(str(99**100)) and len(str(100**99)) will reveal that the first expression results in a length of 200, while the second yields 199. This practical demonstration further supports our conclusions.
If you enjoyed this exploration, you may find the following articles intriguing, and consider following the writer’s Medium profile for more insightful content!
The first video titled "100^99 vs 99^100 which number is bigger? | MATH OLYMPIADS | MATHEMAGIC" provides a visual explanation of the concepts discussed here.
The second video, "Comparing: 100^99 and 99^100, which is larger?" offers additional insights into this mathematical dilemma.