Understanding the Batwing Shape

The unique curves of the batwing figure are generated by sine functions. The task at hand is to determine the area of this intriguing shape. This problem was recently featured in a MathAdam newsletter, where the goal is to compute the area of the batwing figure created from scaled sine waves.

The upper boundary of the figure is defined by the sine function, specifically sin(x), within the range of 0 to π (Equation 1).

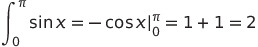
Equation 1 indicates that the area beneath the sine curve is surprisingly an integer rather than just a rational number.

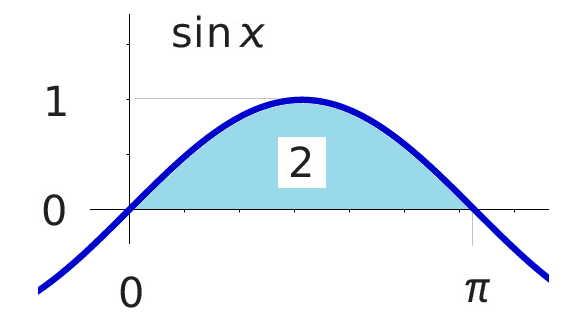
The total area of the batwing shape is constrained to be less than 2. Additionally, we can subtract the area under ½ sin(2x). This integral reflects a variation of the previous calculation, but this area is a scaled-down version of what has just been established. Both vertically and horizontally, the sine wave has been reduced by a factor of one half, leading to a contribution of ¼ of 2.

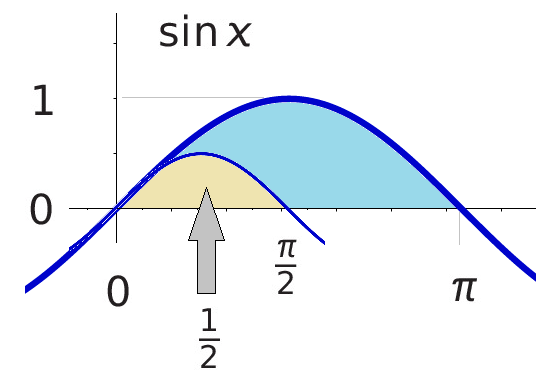
Let’s denote the area we seek as A (Figure 4, top). This shape comprises a smaller version of itself, which we denote as having an area of ¼A (Figure 4, bottom).

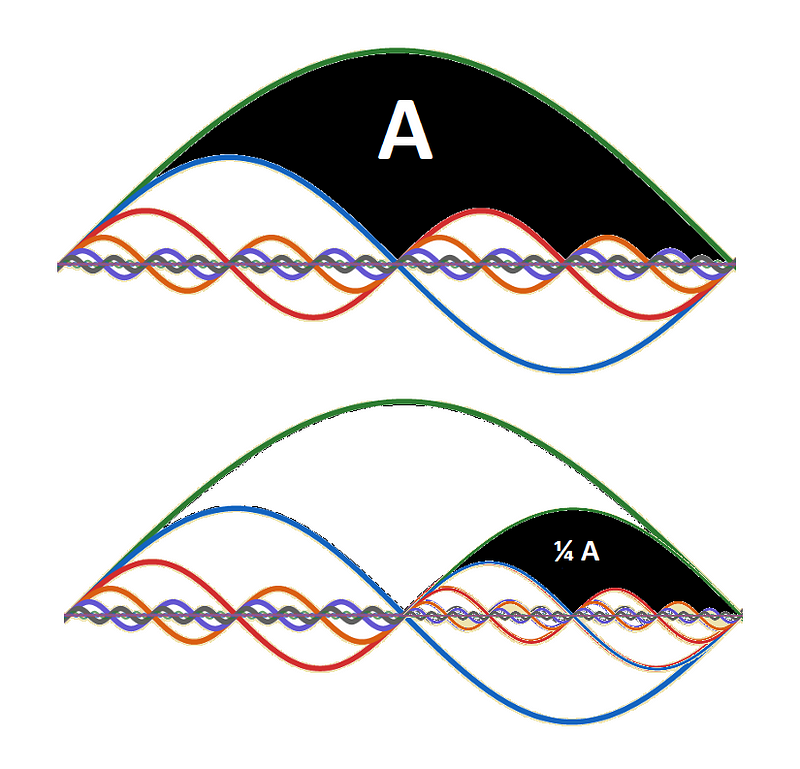
From Figure 1, the area of 2, minus two segments of the area under ½ (from Figure 3), results in a new figure with an area of 1 (Figure 5).

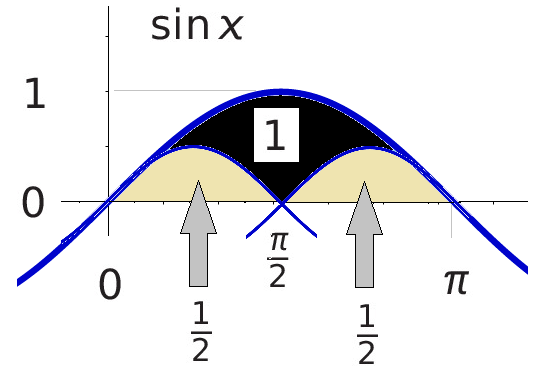
At this point, we have an expression for A, as shown in Figure 4 (top). It is the sum of the areas depicted in Figure 4 (bottom) and Figure 5.

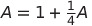
Through some algebraic manipulation, we can derive our final answer:

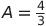
Bob’s Your Uncle.

Improving Arm Strength: Exercises for Seniors

The first video provides a brief 5-minute workout specifically designed to tone arms and eliminate the appearance of "batwings," requiring no weights.

Fixing Batwing Arms with Simple Exercises

The second video showcases three straightforward exercises aimed at seniors to effectively address and improve batwing arms.