Unleashing Your Potential as a Mathematician: The Art of Generalization
Written on
Chapter 1: The Instinct for Generalization
Exceptional mathematicians possess a unique ability to broaden their solutions. This means that when they tackle a specific problem, they instinctively recognize how their findings can be applied to other contexts. This drive to generalize insights is a hallmark of a promising mathematician.
For instance, consider a problem I recently encountered. Suppose you have seven rods, each measuring 1 through 7 units. The challenge is to determine the likelihood that any three selected rods (chosen without replacement) can be arranged to form a non-degenerate triangle, which has a measurable area.

To analyze this, since we’re picking rods without replacement, we’ll assume each rod has a distinct length, represented as a, b, and c, where a > b > c > 0. Here’s a visual representation of the situation.
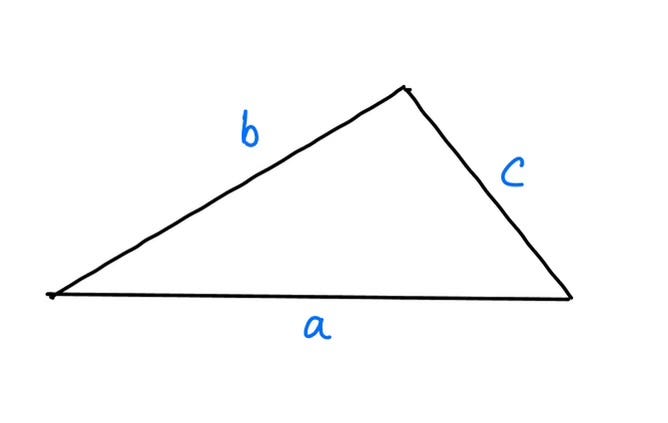
To ensure we can form a non-degenerate triangle, the sum of the lengths of the two shorter rods (b + c) must exceed the length of the longest rod (a). If b + c is less than or equal to a, a triangle cannot be formed.
Thus, we need to identify how many sets of three lengths (a, b, c) exist among the first seven positive integers that satisfy the following conditions:
- a > b > c
- b + c > a
A bit of exploration reveals that the smallest value of a that allows for such a triplet is a = 4. We can systematically calculate as follows:
- If a = 4, then (b, c) = (3, 2)
- If a = 5, then (b, c) = (4, 3) or (4, 2)
- If a = 6, then (b, c) = (5, 4), (5, 3), (5, 2), or (4, 3)
- If a = 7, then (b, c) = (6, 5), (6, 4), (6, 3), (6, 2), (5, 4), or (5, 3)
From this analysis, we find there are 13 combinations of rods that can form non-degenerate triangles. To answer our original question about the probability of randomly selecting three rods that can form such triangles, we need to calculate the total combinations of three rods from our seven:
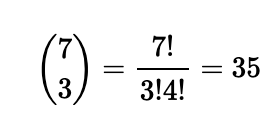
Hence, the probability of forming a non-degenerate triangle with any three chosen rods is 13 out of 35.
Let’s Generalize the Concept
The number seven is not special in this context. We can explore the scenario where we have an odd number of rods, represented as 2N + 1, with lengths from 1 to 2N + 1. We'll apply the same reasoning while abstracting our thought process.
Assume a is the longest rod selected. We know:
- b cannot exceed a - 1
- If a is even, b must be at least (a / 2) + 1, otherwise c would surpass b.
- If a is odd, b must be at least (a + 3) / 2 to prevent c from exceeding b.
Let’s analyze the combinations for both even and odd values of a:

For even a, the total number of combinations is represented by the sum of odd integers: 1 + 3 + 5 + ... + (a - 3).
For odd a, we find the total combinations by summing even integers: 2 + 4 + 6 + ... + (a - 3).
We can now calculate the total number of non-degenerate triangles by starting at a = 4 and going up to a = 2N + 1, applying our formulas for the odd and even cases:
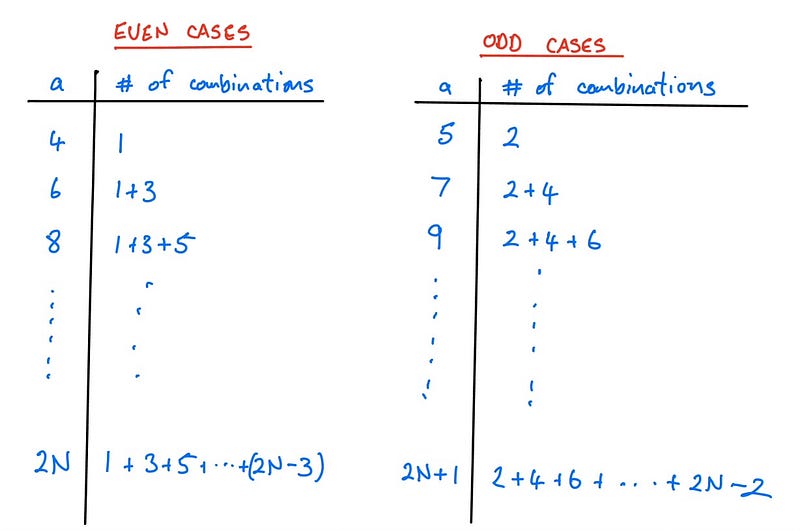
Next, we can sum across rows, which leads to a series of sums for each even integer: 1 + 2, 1 + 2 + 3 + 4, continuing to 1 + 2 + 3 + ... + 2(N-1). Hence, we can express this sum as:
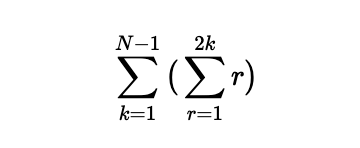
Using the formula for the sum of the first n positive integers (1/2 n(n + 1)), we can simplify this expression further:
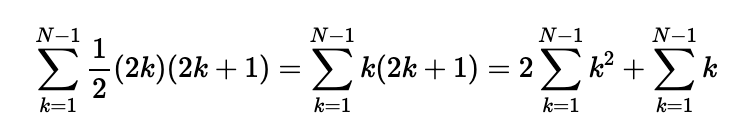
The sum of the first n squares, given by n(n + 1)(2n + 1) / 6, allows us to further condense our expression:
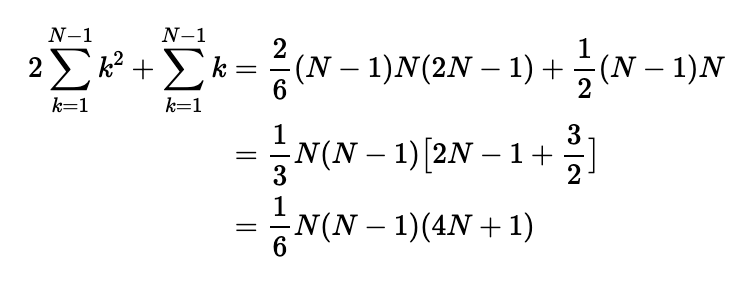
Ultimately, we have derived an expression for the total number of non-degenerate triangles that can be formed when selecting three rods from 2N + 1 rods. To compute the probability, we need the total combinations of three rods from 2N + 1:
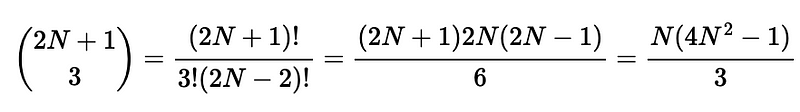
Finally, dividing these two values will yield the probability that any three selected rods can form a non-degenerate triangle:
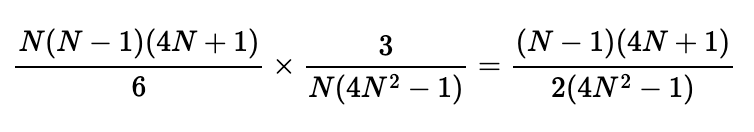
Verifying Our Findings
From earlier calculations, we established that for seven rods, the probability was 13/35. We can validate this by substituting N = 3 into our derived expression, resulting in (2 * 13) / (2 * 35) = 13/35, confirming our result!
Additionally, we can write a function to compute this probability for any odd number of rods:
# Function to calculate probability
def prob_triangle(n: int) -> float:
return ((n - 1) * (4 * n + 1)) / (2 * (4 * (n ** 2) - 1))
# Testing probabilities for various odd rod counts
for n in [3, 5, 10, 100, 1000000]:
print(prob_triangle(n))
This code provides probabilities for scenarios with 7, 11, 21, 201, and 2000001 rods:
>> 0.37142857142857144
>> 0.42424242424242425
>> 0.462406015037594
>> 0.4962499062476562
>> 0.499999625
As the number of rods increases, the probability of selecting three that can form a non-degenerate triangle approaches 0.5, which is consistent with our final expression's limit as N approaches infinity.
What are your thoughts on this problem and the significance of generalizing solutions? Can you think of ways to expand this to include scenarios with an even number of rods? Feel free to share your insights.