Understanding the Exact Value of sin(π/5) in Trigonometry
Written on
Chapter 1: Introduction to Trigonometric Values
In high school pre-calculus, students are introduced to the precise trigonometric values for angles such as 0, π/2, π/3, π/4, and π/6. It might seem unusual that angles like π/5 and π/7 are often overlooked. Occasionally, inquisitive students raise questions about these angles.
Interestingly, sin(π/5) possesses an exact value, though it is more complex compared to sin(π/4) or sin(π/6). By employing the unit circle definition of the sine function, we can derive sin(π/5) using a regular pentagon. In this context, sin(π/5) corresponds to the y-coordinate of the point on the unit circle at the angle π/5, and it can also be represented as half the side length of the inscribed regular pentagon.
Chapter 2: Finding the Length of sin(π/5)
To determine this length, we begin by constructing two isosceles triangles as depicted below. All three segments illustrated in blue are equal in length, which we can label as 'a'.
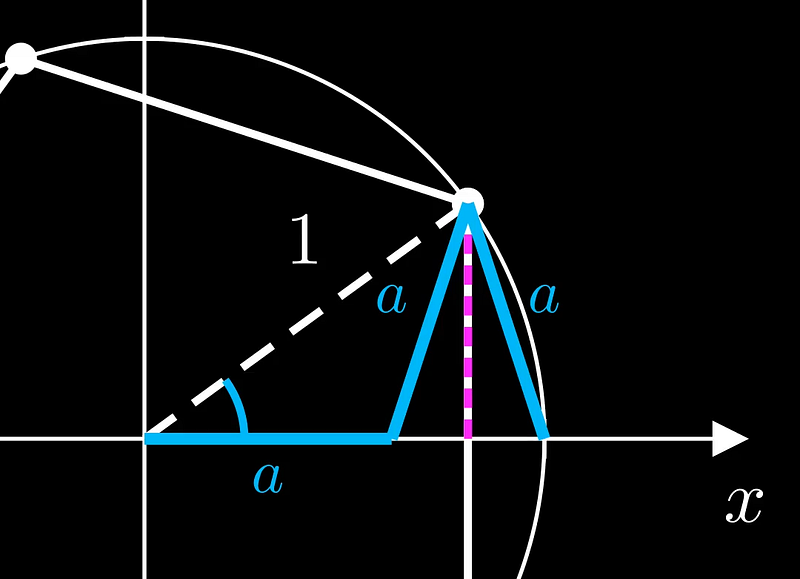
At first glance, the purpose of this might not be evident. However, we are constructing what is known as a “golden triangle.” This isosceles triangle has angles of π/5, 2π/5, and 2π/5, and is closely associated with the regular pentagon.
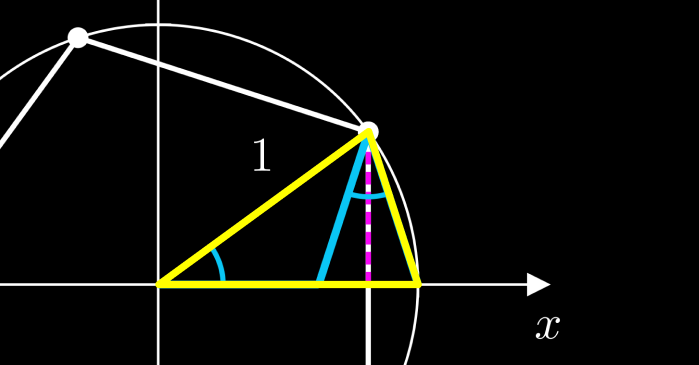
Because the golden triangle contains another similar golden triangle, we can utilize the ratio between the side lengths to formulate an equation, which can be resolved using the quadratic formula.
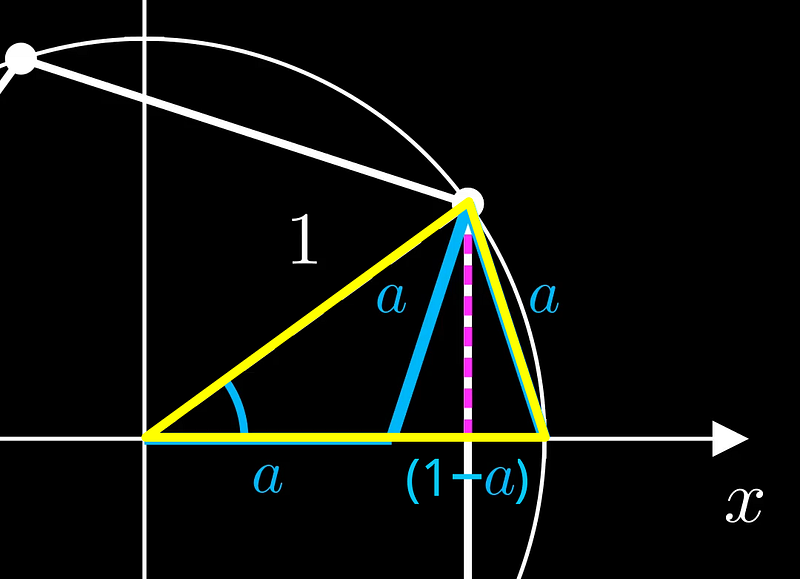
Despite deriving two solutions from the quadratic formula, we select the positive solution for 'a', which evaluates to 1/φ, where φ is the golden ratio, defined as (1 + √5)/2.
Now, we can apply the Pythagorean theorem to ascertain the exact value of sin(π/5), which represents the height of a right triangle with hypotenuse equal to 'a'.
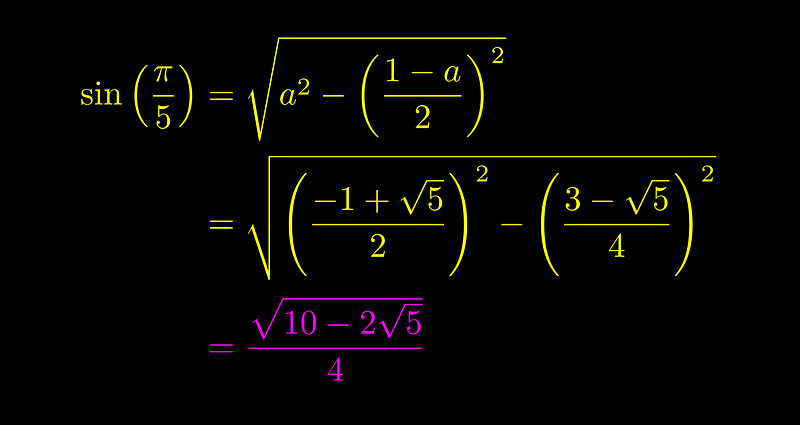
The exact value of sin(π/5) is given by (√(10 - 2√5))/4.
Additionally, if you're curious about sin(π/7), it's noteworthy that this value is not algebraic, meaning it cannot be expressed as the root of any polynomial. This is tied to the fact that a 7-sided regular polygon cannot be constructed using just a compass and straightedge. Conversely, a 17-sided polygon can be constructed, a fact proven by Gauss in his youth. This implies that sin(π/17) is an algebraic number, albeit quite complex!
