Chapter 1: The Parallelogram Challenge

In this exploration, we consider a parallelogram ABCD. Inside this shape, points P and Q are positioned such that triangles ABP and BCQ are equilateral. Our objective is to demonstrate that the intersection of the lines drawn through P, perpendicular to PD, and through Q, perpendicular to DQ, will align with the altitude from B in triangle ABC.

To facilitate our proof, we reference the Theorem Grid, which outlines the various theorems applied throughout this discussion.

Introducing: The Theorem Grid Theorems on Geoclid So Far

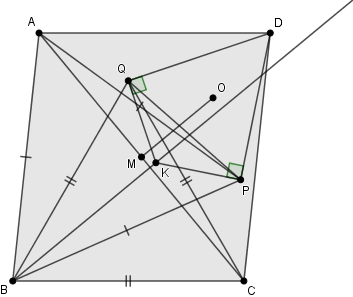
Assume the lines through P and Q that are perpendicular to segments DP and DQ meet at point K. To validate our claim, we must establish that KB is congruent to AC. Let M represent the midpoint of AC, and let γ be the circumcircle of triangle PQD, centered at O. We denote the angle ABC as m, constrained by the condition 60° < m < 120°, as P and Q are located within the parallelogram ABCD.

One notable feature of this configuration is the presence of multiple segments of equal length. Given that ABCD is a parallelogram and both triangles ABP and BCQ are equilateral, we can conclude that CD = AB = BP = PA and DA = BC = CQ = QB.

Furthermore, the angles formed by the parallelogram and the equilateral triangles present equal measures. For instance, angles CDA and ABC are equal to m, while by Theorem 1.3, angle BCD equals angle DAB, which is 180° - m. Thus, we have:

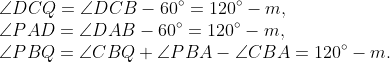
Given that CD = BP = PA and DA = CQ = QB, applying Theorem 1.1 leads us to conclude that triangles DCQ and PAD are congruent to triangle PBQ, which indicates that triangle PQD is equilateral.

Next, let γ intersect lines QK and PK at points K’ and K’’. By Theorem 1.11, we know that DK’ and DK’’ serve as the diameters of γ, forcing K’ and K’’ to coincide at K. Consequently, O becomes the midpoint of DK.

Recall that M is the midpoint of AC. Since ABCD is a parallelogram, Theorem 1.9 confirms that M is also the midpoint of BD. With O as the midpoint of DK and M also as the midpoint of BD, Theorem 1.1 tells us that triangles DOM and DKB are congruent, hence OM is parallel to KB.

Let’s pause for a moment to strategize our next steps. If we can demonstrate that OM is parallel to AC, then using OM parallel to KB, we will ultimately establish that KB is parallel to AC. But how do we achieve this?

Let’s retrace our steps. The assertion that OM is parallel to AC can stem from OA = OC or not. However, a well-crafted diagram may suggest a viable hypothesis. So, how do we derive OA = OC? Are there congruent triangles involving OA and OC?

We have already established that AD = CQ. Since O is the center of γ, we also have DO = QO. Thus, are triangles ODA and OQC the congruent pair we seek? Let’s investigate further.

We will show that triangles ODA and OQC are congruent. Since AD = CQ and DO = QO, we need only to confirm that angles ODA and OQC are equal. Initially, since OP = OQ = OD represents the radius of γ, by Theorem 1.1, angles ODP and OQD are equal, specifically 30°. Recall that angles PDA and DQC are congruent due to the established equality of triangles DCQ and PAD. Therefore,

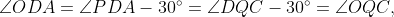
This verifies that triangles ODA and OQC are congruent.

So, what’s next? We simply need to reverse the logical steps we outlined earlier. Since triangles ODA and OQC are congruent, OA equals OC, leading us to conclude that, by Theorem 1.2, OM is parallel to AC. Consequently, since OM is parallel to KB and also to AC, we establish that KB is parallel to AC.

Endnote This problem involves intricate logical reasoning, which adds to its enjoyment and enriches our understanding of the theorems we have encountered thus far.

The quadrilateral PDQK is so unique that it has a special designation: a cyclic quadrilateral. This figure possesses many fascinating properties and is a powerful concept we will explore further in due time.

Stay tuned!

Thank you for your interest! If you appreciate this exploration and wish to support my writing endeavors, consider becoming a member. For just $5 a month, you’ll gain unlimited access to all stories on Medium. If you sign up using my link, I’ll receive a small commission.