A Fun Geometry Challenge with Concentric Circles
Written on
Understanding Concentric Circles
In the realm of geometry, the term "concentric" refers to circles that share the same center. Much like three points are considered collinear if they lie on the same straight line, two circles are termed concentric if they have a common center.
This puzzle is an intriguing challenge that evaluates your grasp of basic geometric principles.
Here’s a suggestion: tap into your creative side and draw out the problem! I encourage you to pause here, grab some paper and a pen, and attempt to solve it. Once you feel prepared, continue reading for the answer!
Solution Unveiled
To begin, we will label the radii of the larger and smaller circles as R and r, respectively, and denote the center of the circles as O.
The crucial step is to draw the radius OA of the larger circle and extend a perpendicular line from O to the line segment AB.
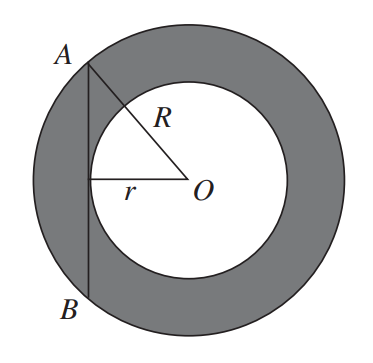
The perpendicular line from O to AB will equal the radius of the smaller circle, denoted as r. Consequently, the area of the shaded region corresponds to the area of the larger circle minus that of the smaller circle.

Mathematically, this can be expressed as follows:
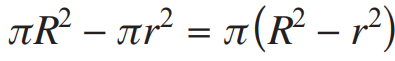
Do you observe something familiar on the right side of this equation? Remember, since AB measures 32, half of AB is 16.
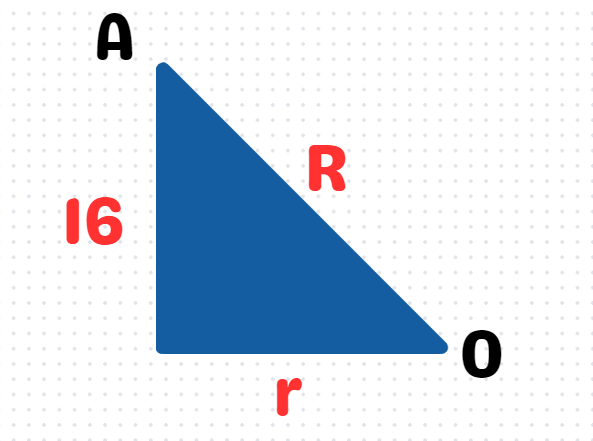
By examining the right-angled triangle, we can deduce that R² - r² = 16² = 256, according to the Pythagorean theorem!
Thus, the area is calculated as 256, leading us to conclude that k = 256.
And there you have it—what a fascinating result!
What was your thought process while tackling this puzzle? I’d love to hear your insights in the comments below!
Best Math Puzzles Compilation
For those interested in further challenges, check out this collection of the best math puzzles available on Medium.
The first video titled "Find area of the Blue shaded Ring | Concentric circles | Annulus | Donut" provides a visual explanation of how to find the area of shaded regions in concentric circles.
The second video, "The Concentric Circles Problem - Math Olympiad Tutorial," offers a tutorial that dives deeper into the complexities of concentric circles and presents strategies for solving related problems.
Thank you for reading! If you found this article helpful, please give it a clap to show your appreciation.
