Chapter 2: The Connection Between Fibonacci and the Golden Ratio

Recognizing that the golden ratio is closely linked to the conversion factors allows us to express the relationship between miles and kilometers as an approximation.

To illustrate this connection, we will utilize Binet’s formula, which involves the Fibonacci sequence (F(n)) and the golden ratio (φ).

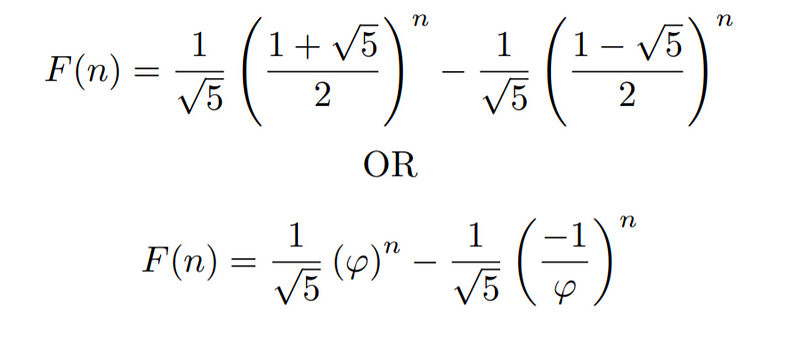
For those interested in the derivation of Binet’s formula, I have previously published an article on the topic.

Next, we will analyze the ratio of consecutive Fibonacci numbers to reveal how φ emerges from the sequence.

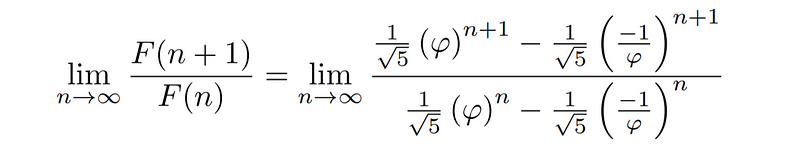
As we pursue this limit, we note that since 1/φ is less than 1, it approaches 0 as n increases. This simplification allows us to focus solely on the dominant terms.

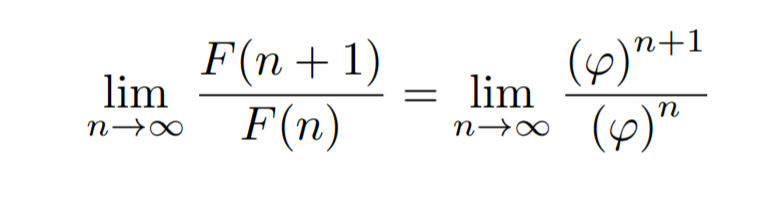
This leads to an approximation that resembles the golden ratio closely.

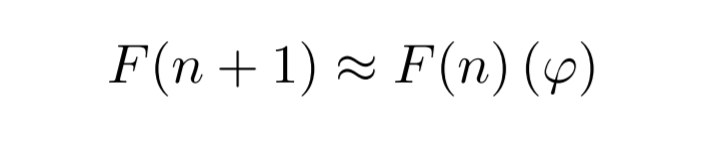
Chapter 3: Practical Applications of Fibonacci in Conversions

To illustrate the Fibonacci sequence further, consider the series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etc. The approximation indicates that multiplying a Fibonacci number by φ is roughly equivalent to identifying the subsequent Fibonacci number.

For example, to convert 5 miles to kilometers, we find the nearest Fibonacci number, which is 8. Thus, we can approximate that 5 miles equals about 8 kilometers, although the precise conversion is 5 miles = 8.04672 km.

What if we attempt to convert 10 miles? Since 10 isn't a Fibonacci number, we can express it as the sum of Fibonacci numbers (8 + 2). This gives us (8 + 2) mi = (13 + 3) km, yielding approximately 16 km. The exact conversion is actually 10 mi = 16.0934 km.

Now, let's look at converting kilometers to miles. Dividing by φ helps us find the preceding Fibonacci number. For instance, converting 42 km to miles involves splitting 42 into Fibonacci components (34 + 8) km = (21 + 5) mi, resulting in approximately 26 mi. The exact conversion is 42 km = 26.0976 mi.

The first video titled "Using Fibonacci to Convert Miles to Kilometers" offers a practical demonstration of this concept, illustrating the conversion process using Fibonacci numbers.

Additionally, the second video, "Fibonacci's Secret: Convert Miles to Km like a Mathematician (Proof by Desmos) #SoMEpi," provides a deeper dive into these mathematical connections.

Chapter 4: Conclusion and Future Insights

While this method may not constitute rigorous mathematics, it reveals an intriguing relationship arising from a closer examination of numbers. The serendipitous connection between the golden ratio and the Fibonacci sequence in the context of distance conversion is a testament to the beauty found within mathematical randomness.

Thank you for joining me on this exploration! I look forward to delving deeper into the wonders of the Fibonacci sequence in future discussions. For further reading, you might enjoy my article titled "Why does 1/89 represent the Fibonacci sequence?"