Chapter 1: The Nature of Observation

As Werner Heisenberg famously stated, “What we observe is not nature itself, but nature exposed to our method of questioning.” This profound insight underscores that our perception of the universe is fundamentally shaped by our observational methods. Quantum mechanics has revealed the limitations of our previous understanding, unveiling a realm filled with uncertainties and new possibilities.

In 1926, Heisenberg embarked on developing a theory rooted in wave mechanics. His efforts to comprehend this novel universe led him to a startling conclusion: it is impossible to measure both the position and velocity of a particle simultaneously. Regardless of the methods employed, this dual measurement remains elusive.

Heisenberg’s insights suggest that the observer inevitably influences the experiment, a notion illustrated by the double slit experiment. He posited that the inability to measure both velocity and position concurrently is a fundamental characteristic of subatomic particles, a revelation that sent ripples through the physics community.

Heisenberg's Early Insights

At just 26 years of age, Heisenberg articulated these revolutionary ideas. The scientific community held onto the hope that there existed a framework capable of explaining the erratic behaviors of particles, which had long been governed by classical physics. Traditionally, the laws of the universe were perceived through the lens of mathematics—a language believed to provide answers to all mysteries.

Quantum mechanics introduced the idea that determining both the precise velocity and position of a particle is impossible. In essence, particles exhibit both wave-like and particle-like behaviors, complicating our comprehension of them.

Today's physics acknowledges that every particle possesses a wavelength, albeit so minuscule that it escapes our naked eyes. Just how small are these wavelengths?

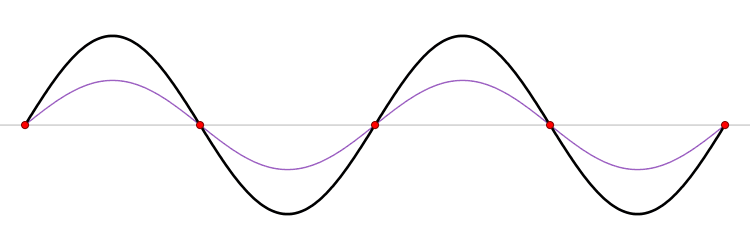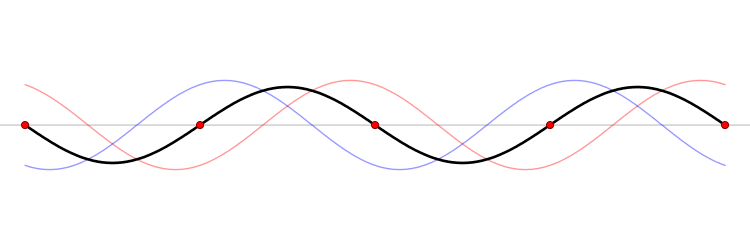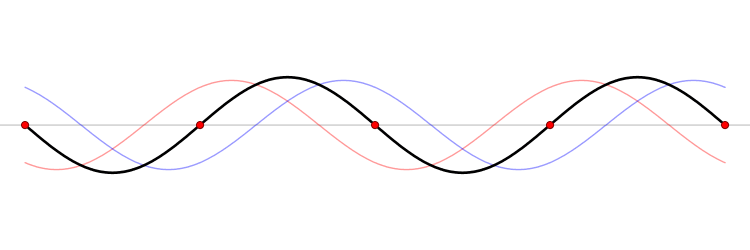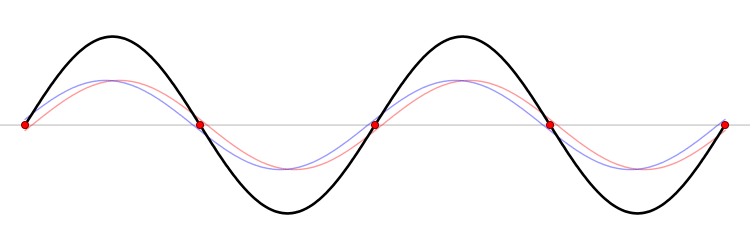
The connection between momentum and wavelength for matter waves can be expressed as ( p = h/? ) (de Broglie's hypothesis), where ( p ) signifies momentum and ( h ) represents Planck’s constant. De Broglie’s equations highlight that a particle's wavelength is inversely related to its momentum, which leads us to consider Planck’s constant.

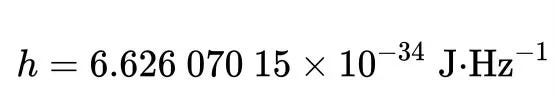
The Planck constant, which has dimensions of angular momentum, is measured in joules per hertz (J·Hz⁻¹) or joule-seconds (J·s). Hence, as momentum rises, the corresponding wavelength diminishes to infinitesimal values.

In terms of momentum, we denote it as ( p = m cdot v ); thus, increases in mass and velocity parallel increases in momentum. Consequently, as a particle becomes smaller, its wavelength expands, resulting in greater uncertainty.

For instance, humans also possess a wavelength since we are composed of atoms. However, this wavelength is imperceptible, leading to negligible uncertainty in our movements—making it clear, for example, where we will land if we trip or are pushed.

The unpredictable nature of particle behavior permeates the universe, revealing the inadequacies of classical physics. Quantum mechanics, in contrast, presents a universe brimming with possibilities. But does this uncertainty imply we cannot ascertain anything with precision? Not quite.

Quantum Probability and Its Implications

We can make informed approximations. Erwin Schrödinger, recognized for his famous thought experiment involving Schrödinger's cat, introduced quantum probability. His equation forecasts the wave motion of particles.

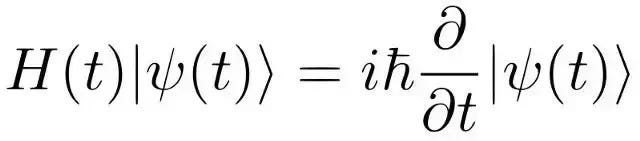
This intricate equation essentially indicates the probable locations of particles, known as the probability density function—referred to as the Schrödinger equation. This formulation also prompted a shift in Niels Bohr’s classical atomic model.

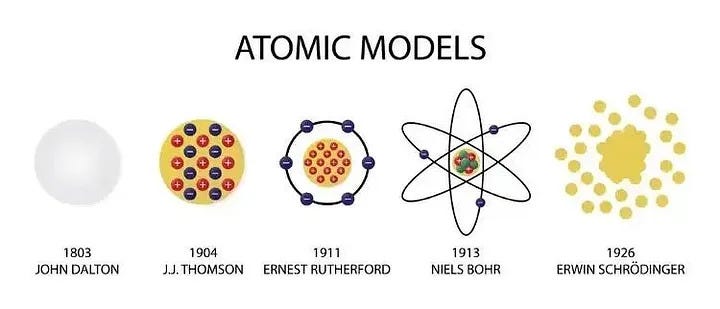
The uncertainty principle indicates that one cannot pinpoint an electron's exact position around the nucleus, leading to a model characterized by a diffuse area where the electron may be found. Schrödinger’s equation permits us to calculate this probability. Nevertheless, this is where significant disputes within quantum mechanics arise.

“I don’t like it, and I’m sorry I ever had anything to do with it.” — Erwin Schrödinger

Prior to measurement, an electron exists throughout this "cloudy" region, a phenomenon known as quantum superposition—where a particle can occupy multiple locations, evident in experiments like the double slit or Schrödinger’s cat. Ultimately, measurement merely narrows down the likelihood of locating the electron, forcing it into a specific position.

This is where Heisenberg's insights become crucial: “You’ve measured the particle and constrained it to a location, but your measurement is not infallible.”

Heisenberg’s Uncertainty Principle

Heisenberg's uncertainty principle states that regardless of the measuring device's precision, the position or momentum of a particle can only be known within a certain limit. If one seeks exact position details, momentum becomes elusive, and vice versa.

In essence, this principle suggests that predicting a quantity with absolute certainty is unattainable, even when all initial conditions are accounted for.

This encapsulates Heisenberg's universe: the mathematics we employ and the universe we perceive diverge significantly.

All matter in the cosmos consists of these uncertain, unpredictable particles. Surprisingly, an invisible connection links all these particles. While the universe may appear chaotic, it embodies an inherent order.

Classical physics might lead to atheism, but understanding the universe through quantum mechanics can alter that perspective.

“The first gulp from the glass of natural sciences will turn you into an atheist, but at the bottom of the glass, God is waiting for you.” — Werner Heisenberg

References

• CODATA Value: Planck constant. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2021–04–28.
• Schrödinger, E. (1926). An Undulatory Theory of the Mechanics of Atoms and Molecules, Physical Review. 28 (6): 1049–1070.
• Werner Heisenberg, The Physical Principles of the Quantum Theory, p. 20.

Chapter 2: Understanding the Uncertainty Principle

This video, titled "Demystifying the Heisenberg Uncertainty Principle," explores the core concepts and implications of Heisenberg's groundbreaking idea, offering insights into how it reshaped our understanding of quantum mechanics.

In this video, "What is the Heisenberg Uncertainty Principle? - Chad Orzel," the presenter breaks down the principles behind Heisenberg's theory, making it accessible for those new to the subject.