Chapter 1: Understanding the Problem

In triangle ABC, let BE and CF represent the internal angle bisectors of angles B and C, respectively, with points E located on side AC and F on side AB. Consider a point X on segment CF such that line AX is perpendicular to CF. Similarly, let Y be a point on segment BE where line AY is perpendicular to BE. Our goal is to prove the relationship:

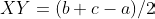
where BC = a, CA = b, and AB = c.

This task involves the concept of similarity in triangles. It is advisable to review Theorem 1.1 if you are not already familiar with it.

Section 1.1: Extending Lines

To proceed, we extend lines AX and AY until they intersect line BC at points X' and Y', respectively. According to Theorem 1.1, we can establish the congruences ∆CXA ≅ ∆CXX' and ∆BYA ≅ ∆BYY', which leads to the following equalities: AX = XX', CA = CX', AY = YY', and BA = BY'. Consequently, we obtain:

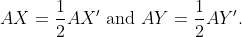
With these relationships, Theorem 1.1 provides the similarity:

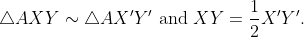
Thus, we conclude:

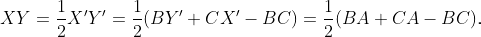
The final equation leverages the previously established equalities BA = BY' and CA = CX'.

Endnote: Utilizing Theorems

We can also demonstrate that BA = BY' and CA = CX' by employing Theorem 1.2. For instance, since BY acts as an internal angle bisector of angle ABY' and is also perpendicular to AY', it follows that triangle ∆BAY' is isosceles, resulting in BA = BY'. A similar argument applies to triangle ∆CAX'.

Moreover, we could utilize Theorem 1.3 for a more straightforward proof. Since we know that ∠BAY = 180° - ∠AYB - ∠YBA = 180° - ∠Y'YB - ∠YBY' = ∠BY'Y, we can directly conclude that BA = BY'. The same reasoning applies to ∆CAX'.

The key takeaway is that these theorems serve merely as tools to help us reach our conclusions. While we can use any theorem for this relatively straightforward problem, selecting the appropriate one becomes crucial for more complex challenges. If you're ever in doubt, experimenting with all available theorems can be a worthwhile strategy.

Thanks for engaging with this content! In our next discussion, we will delve into Pythagoras and the renowned Pythagorean theorem.

Chapter 2: Real-World Applications of Geometry

In this video, titled "A Very Simple Solution to a Maths Olympiad Problem," we explore straightforward methodologies for tackling Olympiad-style geometry problems.

The second video, "CRMO 2012 Problem 4 | Combinatorics and Set Theory | Math Olympiad India," delves into the intricate connections between combinatorial strategies and geometry.